
Wykorzystanie sieci neuronowych do prognozowania szeregów czasowych
22 grudnia 2021
Jak rewolucja AI zmienia biznes
19 stycznia 2022

Wykorzystanie sieci neuronowych do prognozowania szeregów czasowych
22 grudnia 2021
Jak rewolucja AI zmienia biznes
19 stycznia 2022Sieci konwolucyjne

Coraz większa ilość danych jest przechowywana w postaci szeregów czasowych: indeksy giełdowe, dane klimatyczne, testy medyczne, itp. Istnieje wiele metod regresji dla szeregów czasowych. Większość z nich składa się z dwóch głównych etapów: na pierwszym etapie albo używamy jakiegoś algorytmu do pomiaru odległości między szeregami czasowymi, które chcemy badać (np. DTW jest bardzo popularne) lub używamy jakichkolwiek metod aby zmienić reprezentację szeregów czasowych i przedstawić je jako wektory cech. W drugim etapie używamy jakiegoś algorytmu do prognozowania przyszłych wartości szeregu czasowego. Może to być cokolwiek od metody k-najbliższych sąsiadów i SVM do głębokich sieci neuronowych. Jedna rzecz łączy te metody: wymagają pewnego rodzaju inżynierii cech jako oddzielnego etapu przed wykonaniem analizy regresji. Na szczęście istnieją modele, które nie tylko zawierają inżynierię cech w swojej naturze, ale również eliminują konieczność wykonywania jej ręcznie: są w stanie wyodrębnić cechy i stworzyć informacyjne reprezentacje szeregów czasowych automatycznie. Modele te to konwolucyjne sieci neuronowe (CNN). Badania wykazały, że wykorzystanie CNN do regresji szeregów czasowych ma kilka istotnych zalet w stosunku do innych metod. Są one modelami wysoce odpornymi na szumy i są w stanie wyodrębnić bardzo informacyjne, głębokie cechy, które są niezależne od czasu. Celem operacji konwolucji jest wyodrębnienie cech wysokiego poziomu. CNN nie musi być ograniczona do jednej warstwy konwolucyjnej. Konwencjonalnie, pierwsza warstwa jest odpowiedzialna za przechwytywanie cech niskopoziomowych. Po dodaniu kolejnych warstw, architektura dostosowuje się również do cech wysokopoziomowych, dając nam sieć, która w pełni rozumie zbiór danych, podobnie jak my byśmy to robili.
Wyobraźmy sobie szereg czasowy o długości n i wymiarze k. Długość jest liczbą punktów czasowych, a wymiar jest liczbą zmiennych w wielowymiarowym szeregu czasowym. Na przykład, dla szeregu czasowego pogody mogą to być takie zmienne jak temperatura, ciśnienie, wilgotność itp.
Jądra konwolucji (ang. kernel) mają zawsze taki sam wymiar jak szereg czasowy, natomiast ich długość może być zmienna. W ten sposób, jądro porusza się w jednym kierunku od początku szeregu czasowego do jego końca, wykonując konwolucję. Elementy jądra mnożone są przez odpowiednie elementy szeregu czasowego, który w danym momencie obejmują. Następnie wyniki mnożenia są sumowane, a na wartość tę nakładana jest nieliniowa funkcja aktywacji. Otrzymana wartość staje się elementem nowego „przefiltrowanego” jednowymiarowego szeregu czasowego, a następnie jądro przesuwa się do przodu wzdłuż szeregu czasowego, aby wyprodukować następną wartość. Liczba nowych „przefiltrowanych” szeregów czasowych jest taka sama jak liczba jąder konwolucji. W zależności od wielkości jądra, różne aspekty, właściwości, „cechy” początkowego szeregu czasowego są uchwycone w każdym z nowych przefiltrowanych szeregów.
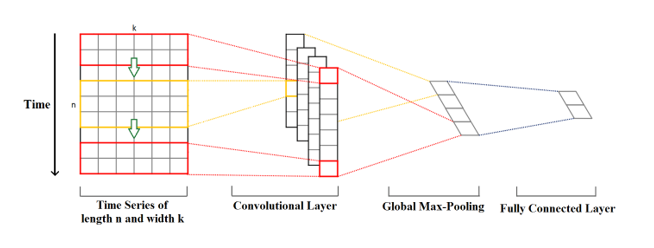
Następnym krokiem jest zastosowanie operacji poolingu (ang. max-pooling) do każdego z przefiltrowanych wektorów szeregów czasowych: największa wartość jest pobierana z każdego wektora. Z tych wartości tworzony jest nowy wektor, a ten wektor maksimów jest ostatecznym wektorem cech, który może być użyty jako wejście do zwykłej, w pełni wypełnionej warstwy (ang. fully conected layer).Rysunek 1. Działanie sieci konwolucyjnej.
Niniejszy artykuł powstał dzięki środkom pochodzącym ze współfinansowania przez Unię Europejską Programu Operacyjnego Inteligentny Rozwój 2014-2020, projektu realizowanego w ramach konkursu Narodowego Centrum Badań i Rozwoju: w ramach konkursu „Szybka Ścieżka” dla mikro-, małych i średnich przedsiębiorców – konkurs dla projektów z regionów słabiej rozwiniętych w ramach Działania 1.1: Projekty B+R przedsiębiorstw Poddziałanie 1.1.1 Badania przemysłowe i prace rozwojowe realizowane przez przedsiębiorstwa. Tytuł projektu: „Stworzenie oprogramowania do poprawy trafności prognoz i optymalizacji zapasów z perspektywy odbiorcy i dostawcy współpracujących w ramach łańcucha dostaw przy zastosowaniu rozmytych, głębokich sieci neuronowych.




OSTATNIE WPISY
TAGI
- #AI
- #bullwhip-effect
- #covid19
- #łańcuch-dostaw
- #NCBiR
- #optymalizacja-zapasów
- #out-of-stock
- #outllier
- #overstock
- #prognozowanie
- #prognozowanie-popytu
- #Program-Operacyjny-Inteligentny-Rozwój-2014-2020
- #projekcja-zapasów
- #projekcja-zapasów-w-czasie
- #service-level-dostawcy
- #sieci-neuronowe
- #supplychain
- #sztuczna-inteligencja-od-A-do-Z
- #zapas-bezpieczeństwa
- #zapas-sezonowy
- #zapas-zabezpieczający
- #zarządzanie-zapasem
Powiązane wpisy
D jak Dead Stock
PRZECZYTAJ
Dead stock, czyli dosłownie martwy zapas, to produkty, które nie znajdują nabywców w oczekiwanym czasie lub w ogóle nie są sprzedawane. Wpływa to negatywnie na efektywność […]
C jak cash to cash cycle
PRZECZYTAJ
Cykl cash to cash cycle to okres pomiędzy momentem, w którym firma płaci swoim dostawcom za zapasy, a otrzymaniem gotówki od klientów. Koncepcja ta służy do […]
B jak Break-event-point
PRZECZYTAJ
Metoda punktu równowagi (break-even point) jest narzędziem wykorzystywanym do optymalizacji zapasów w łańcuchu dostaw. Jest to punkt, w którym koszty posiadania zapasów równają się korzyściom z […]


